Class inheritance


In this section we provide information that help understanding the aspects of the object oriented programming used for PRM. Before going further in our theoretical description of the concept, we have to show to the reader why PRM ensure a flexible class inheritance mechanism comparing to OOBN (Torti et al. (2010),Torti (2012)). Indeed, In OOBNs, we must push out of a class its output attribute, i.e., the user must declare what attributes in a class can be accessed by other classes. While in PRM classes pull from other classes any required attribute, i.e., an attribute becomes an output attribute when the user adds a child from another class to that attribute. OOBN’s input attributes are replaced in PRMs by slot chains.

1. Simple class inheritance

A class \(Z\) is a subclass of class \(X\), denoted \(X \rhd Z\), if:

  • For each attribute \(X.A \langle \tau_{X.A} ,\pi(X.A),\phi_{X.A}\rangle\) there exists an attributes \(Z.A \langle \tau_{Z.A} ,\pi(Z.A),\phi_{Z.A}\rangle\) such that \(\tau_{X.A}= \tau_{Z.A}\).

  • For each reference slot \(X.\rho= \xi\), there exists a reference slot \(Z.\rho= \zeta\) such that \(\xi=\zeta\),

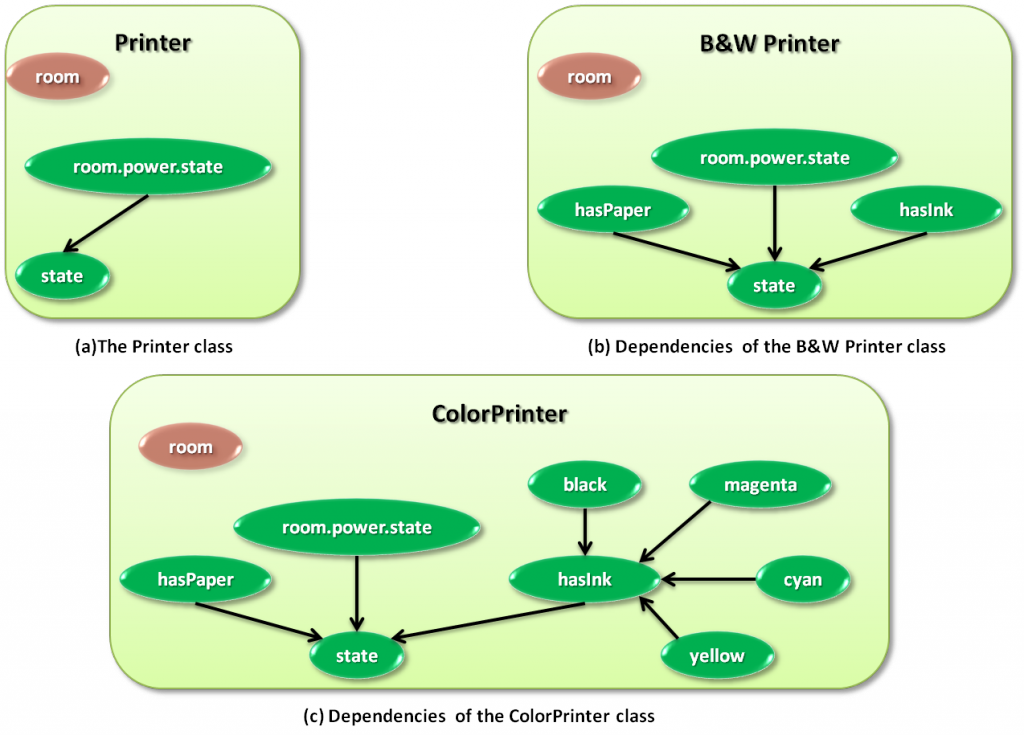
Figure 1 illustrates three classes: Printer (figure 1.a), B&W Printer (figure 1.b) and Color Printer (figure 1.c). Color Printer is a subclass of B&W Printer, which is a subclass of Printer. We can see that any attribute existing in Printer is present in either of its subclasses. We notice that attributes parents nor conditional probability distributions are preserved. Indeed, the set of parents of attribute state changes. Consequently its conditional probability distribution changes from class Printer to class B&W Printer. The same happens for attribute hasInk in class Color Printer, but not for attribute hasPaper which is identical to its version in class B&W Printer.

Figure 1: Example of class inheritance (green nodes are attributes and red nodes are reference slots)
Figure 1: Example of class inheritance (green nodes are attributes and red nodes are reference slots).

2. Attribute’s type specialization

Attribute’s type's inheritance purpose is to provide an additional behaviour specialization to class inheritance. In fact, this notion helps modelling hierarchically structured variables that share a common domain in BN. In section of simple class inheritance, we have seen that it only allows changing inherited attributes conditional probability distributions, i.e., we can add and/or remove parents or just change their conditional probability distributions. This feature, yet useful, does not provide total satisfaction. Indeed, when specializing a class we often want to model new states that are specific to the subclass. For example, in the power surge example we could consider the following type for Printer’s state attribute: {functional, dysfunctional, and broken} is a subtype. The two values dysfunctional and broken are specific to printers: dysfunctional indicates that the printer prints but badly or is suffering some minor issue, e.g., a colour is missing or the paper tray is empty. Broken states that the printer does not print anymore, there could be a paper jam or an internal component broken. In other words, OK and NOK can be decomposed into functional, malfunctioning and broken In some cases we can cope with such specialization by adding new attributes, but in others we may want to overload attributes with specialized types Attribute subtyping can be modeled using a function mapping a subtype values to a subset of the super type values. Such functions are called domain generalization functions, since they generalize concepts present in subtypes.

2.1 Domain generalization function

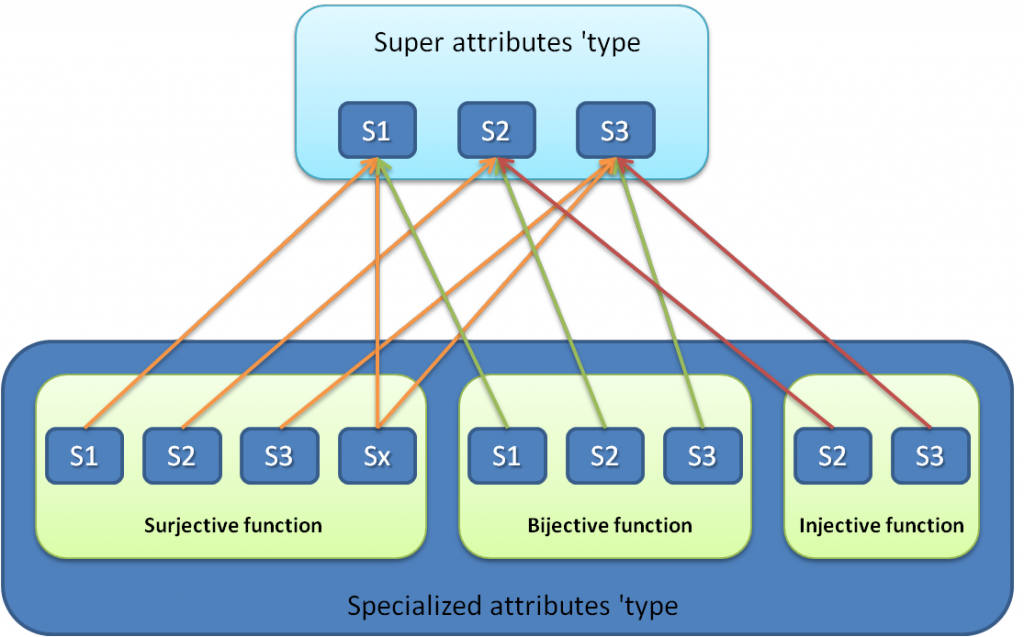
A domain generalization function is a function \(\phi : \tau \rightarrow P(\lambda)\) where \(\tau\) and \(\lambda\) are two distinct attribute types and \(P(\lambda)\) is a subset of \(\lambda\)'s values. Furthermore, domain generalization function can have one of the three following forms : bijection, surjective or injective function. For example, let us consider a disease with different variations. The set of all possible symptoms is {S1,S2,S3}. Each specialized variation may not present necessarily all the three symptoms, it could have a subset of them or it includes new symptoms.

Figure 2: Forms of domain generalization function
Figure 2: Forms of domain generalization function.

2.2 Attribute typing inheritance

An attribute type \(\tau\) inherits from another attribute type \(\lambda\) , denoted \(\lambda \rhd \tau\), if it is defined using a domain generalization function \(\phi : \tau \rightarrow P(\lambda)\). We say that \(\lambda\) generalizes \(\tau\) or that \(\tau\) specializes \(\lambda\).

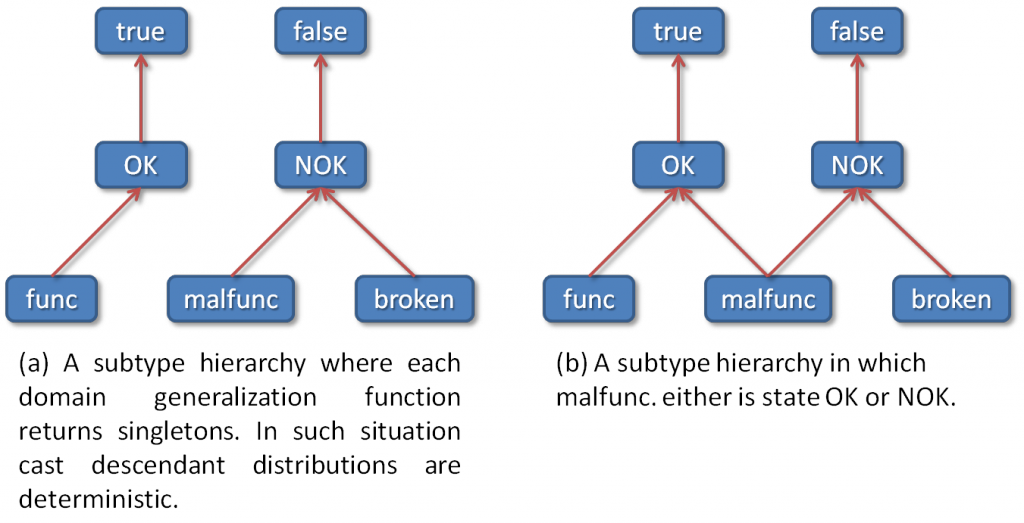
A type hierarchy with attribute types boolean, t_state and t_malfunction.
Figure 3: A type hierarchy with attribute types boolean, t_state and t_malfunction.

Figure 3 illustrates type inheritance. Arcs represent concepts specialization. For example, t_malfunction has three values: functional (func),malfunction (malfunc) and broken. In figure 3.a,functional and malfunction are specialization of NOK. In figure 3.b an alternative representation is illustrated and malfunction is also a specialization of OK. As is, attribute’s type inheritance is only a semantic relation: t_state’s label OK is a sort of true, broken is a sort of false, etc.

2.3 Attribute overloading

Attribute’s type inheritance represents the specialization mechanism for overloading attributes. If we overload attributes with different types, we will obviously break probabilistic dependencies. If a class \(C\) depends on \(D\)’s attributes and that we connect an instance of \(C\) with an instance of \(E\), such that \(D \rhd E\) and that some of \(E\)’s attributes specialize \(D\)’s, then \(C\)’s instance dependencies will be broken. Indeed, by changing the domain of the underlying random variables, all conditional probability distributions specifications become erroneous. However, preserving dependencies is a must. To do so, we suggest cast descendants method as a solution that allows attribute overloading using type inheritance and that preserves dependencies.

2.4 Attribute type genealogy

The genealogy of an attribute’s type \(\tau\) is a set of attribute’s types \({\lambda_1,...,\lambda_n}\) such that \(\lambda_1 = \tau\) and \(\lambda_{i+1} \rhd \lambda_i\) for \(1 \leq i \lt n\) where \(\lambda_n\) is a type with no super type, called \(\tau\)’s ancestral type.

A type’s genealogy is an ordered set of all the type’s super types. We will exploit types genealogies to automatically generate cast descendant attributes. These cast descendant attributes purpose is to cast an attribute into one of its super types. Cast descendants are automatically added, such that any attribute can be cast in any of its super types. Suppose that we have two classes \(X\) and \(Y\) such that some attribute in \(X\) is overloaded in \(Y\) using type specialization. If a third class, name it \(Z\) has an attribute with a parent \(K.A = C.A\) then the slot chain \(K\) can reference an instance of \(Y\) by changing \(K.A\) to \(K.A'_i\).

Consequently, slot chains will automatically be plugged to attributes of the correct type, see
figure 4
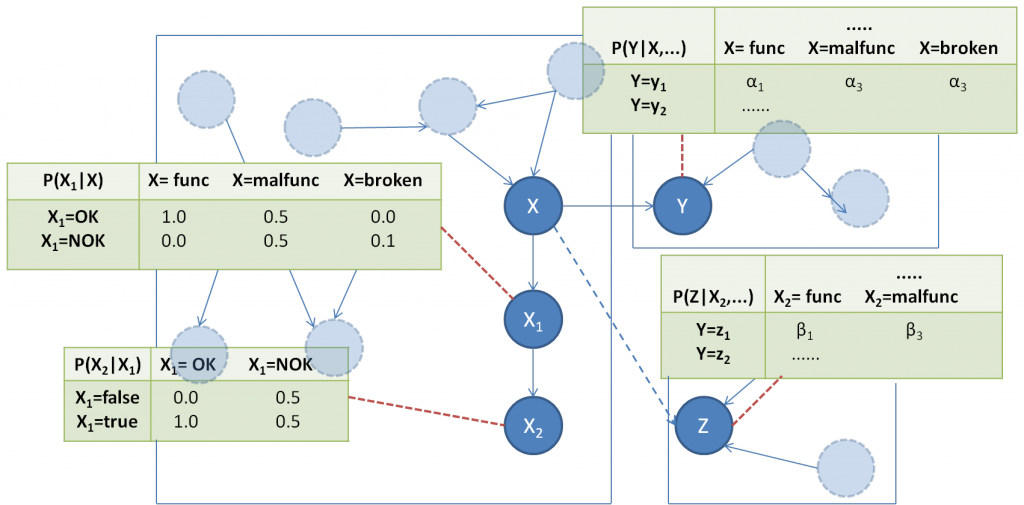
Figure 4: X is an attribute with two cast descendant (X1 and X2 ). Attributes Y and Z both depends on X, however Z expects a boolean while Y expects an attribute of type t_malfunction.

Figure 4: X is an attribute with two cast descendant (X1 and X2). Attributes Y and Z both depends on X, however Z expects a boolean while Y expects an attribute of type t_malfunction.

for an example. The cost of adding cast descendants is negligible because if they are not used, i.e., neither queried nor referenced by a slot chain, we can discard them before inference as they will be barren nodes.

3. Cast descendant

Let \(X.A = \langle \tau ,\pi(X.A),\phi_{X.A}\rangle\) be an attribute with \(\tau\)’s genealogy being \({\lambda_1,...,\lambda_n}\). \(X.A\) cast descendants are the set of attributes:

$$\{X.A'_i=\langle \lambda_i ,\pi(X.A'_{i-1}),\phi_{X.A'_i}\rangle\}$$

with \(1 \leq i \leq n\)' and \(X.A'_0 =X.A\) is either user defined or the default cast distribution. We say that \(X.A_i\) is the direct cast descendant of \(X.A_{i-1}\).

3.1 Default cast distribution

Let \(\tau = \{l^{\tau}_1,...,l^{\tau}_n\}\) and \(\lambda= \{l^{\lambda}_1,...,l^{\lambda}_n\}\) be two attribute types of respective domain sizes \(n\) and \(m\) such that \(\lambda \rhd \tau\), Given an attribute \(X.A= \langle \tau ,\pi(X.A),\phi_{X.A}\rangle\), its direct cast descendant \(X.A = \langle \tau ,\pi(X.A),\phi_{X.A}\rangle\) and the domain generalization function: \(\tau \rightarrow P(\lambda)\), the default cast distribution for \(P(X.A'|X.A)\) is:

$$P(X.A_{\lambda}=l^{\lambda}_i|X.A=l^{\tau}_j)=\begin{cases}\frac {1}{|\phi(l^{\tau}_j)|}, & \text{if }l^{\lambda}_i\in\phi(l^{\tau}_j)\\0, & \text{ otherwise} \end{cases}$$

Figure 4 illustrates an example of cast descendants using the default cast distribution with the domain generalization functions of figure 3.b A type hierarchy with attribute types boolean, t_state and t_malfunction. . Attribute \(X\) is of type t_malfunction, \(X_1\) of type t_state and \(X_2\) of type boolean. Figure 4 shows a partial representation of a system in which three instances are connected through dependency links \(X \to Y\) and \(X_2 \to Z\). Attributes \(Y\) and \(Z\) are both connected to \(X\) using a slot chain, but where \(Y\) expects an attribute of type t_malfunction, \(Z\) expects type boolean. \(Z\)’s class must be connected to some super class of \(X\)’s one and \(X\) must be an overloading using type specialization. The framework can easily detect that \(Z\) requires a subtype of \(X\), and automatically connects it to the correct cast descendant.

Figure 4: X is an attribute with two cast descendant (X1 and X2 ). Attributes Y and Z both depends on X, however Z expects a boolean while Y expects an attribute of type t_malfunction.
Figure 4: X is an attribute with two cast descendant (X1 and X2 ). Attributes Y and Z both depends on X, however Z expects a boolean while Y expects an attribute of type t_malfunction.

4. Subtype polymorphism and dependencies preservation

In the precedent section we have mentioned subtype polymorphisms and we will now explain how such feature can be added to PRM’s class inheritance scheme.

4.1 Relational Skeleton with subtype polymorphism

A relational Skeleton \(\sigma\) is a set of instances such that for any instance \(i\) of class \(X\) and any reference slot \(X.\rho = \epsilon\), there exists at least one instance \(j\) in \(\sigma\) such that \(j\) is an instance of \(\epsilon\) or of a subclass of \(\epsilon\) and \(j \in range (i.\rho)\).

Now, we allow a wider range of instances to be referenced by reference slots. Another important feature regarding reference slot and class inheritance is the possibility of overloading reference slots. Reference slot overloading consists in specializing the range of an inherited reference slot. This is a useful feature when modelling complex systems as we will often first define classes using abstract concepts and specialize them using inheritance. In many cases we want to increase the complexity of the relationships between classes. We can now provide a proper definition of class inheritance in PRMs.

5. Advanced class inheritance

A class \(Y\) is a subclass of class \(X\), denoted \(X \rhd Y\) if:

  • For each attribute \(X.A = \langle \tau_{X.A} ,\pi(X.A),\phi_{X.A}\rangle\), there exists an attribute \(Y.A = \langle \tau ,\pi(Y.A),\phi_{Y.A}\rangle\) such that \(\tau_{X.A}=\tau_{Y.A}\) or \(\tau_{X.A} \rhd \tau_{Y.A}\)

  • For each reference slot \(X.\rho=\xi\), there exists a reference slot \(Y.\rho=\zeta\) such that \(\xi=\zeta\) or \(\xi \rhd \zeta\).

The fundamental property that must be present in any class inheritance mechanism is dependencies preservation. Preserving dependencies guarantees subtype polymorphism as it states that wherever a class is used in defining a probabilistic dependency, we can replace it by one of its subclasses without requiring to change any attribute or reference slot definition.

5.1 Dependencies preservation

Let \(X\) and \(Y\) be two classes such that \(X \rhd Y\). For each reference slot \(\rho^X \in R(C)\), we denote \(\rho^Y\) its inherited version in \(Y\) and for each attribute \(A^X \in A(X)\), we denote by \(A^Y\) its inherited version in \(Y\). A class inheritance mechanism preserves dependencies if:

  • For any slot chain \(K = \{\rho_1,...,\rho^{X}_i,...,\rho_n\}\), we can substitute \(X\) referenced by \(\rho_{i-1}\) by \(Y\) such that \(K'=\{\rho_1,...,\rho^{Y}_i,...,\rho_n\}\) is a legal slot chain.

  • For any parent \(K.X\) with \(K = \{\rho_1,...,\rho^{X}_n\}\), we can substitute \(X\) referenced by \(\rho_{n-1}\) by \(Y\) such that \(K' = \{\rho_1,...,\rho^{Y}_n\}\) is a legal slot chain and \(K'.A\)'s type equal or is a subtype of \(K.X\)’s type.

An illegal slot chain would be a slot chain \(X.K= \{\rho_1,...,\rho_n\}\) such that \(\exists \rho_i \in X.K , \rho \notin R(X.\rho_1,...,.\rho_{i-1})\).

Semantics and definitions
Inference in PRM

Bibliography

Lionel Torti. Inférence probabiliste structurée dans les modèles graphiques probabilistes orientés-objet. PhD thesis, Université Pierre et Marie Curie (UPMC), 2012. ↩

Lionel Torti, Pierre-Henri Wuillemin, and Christophe Gonzales. Reinforcing the Object-Oriented Aspect of Probabilistic Relational Models. In PGM 2010 - The Fifth European Workshop on Probabilistic Graphical Models, 273–280. September 2010. URL: http://www-desir.lip6.fr/~gonzales/research/publications/pgm10.pdf. ↩