The printers example
In this section we propose a tutorial as an application example, the O3PRM documentation helps the reader to understand the functions used for modelling.
1. The printers example
Let's recall the Printers example :
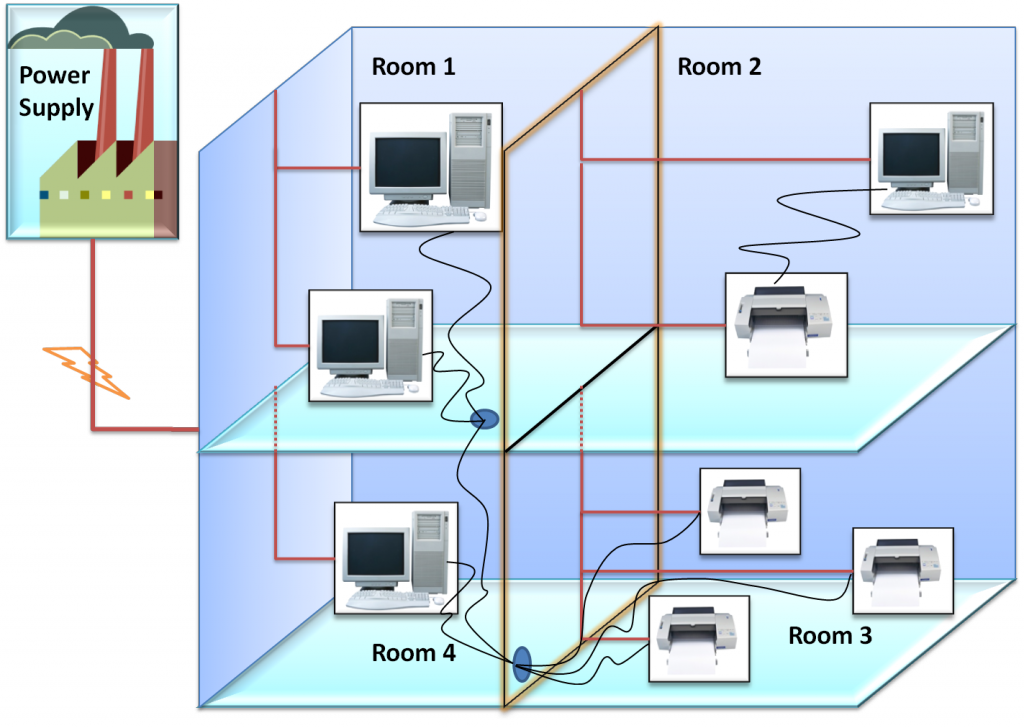
The printers example is a computer maintenance problem where a set of computers and printers, located in different rooms, are powered by one or more power supplies. Depending on the voltage spike intensity and the overall quality and age of electronic devices, computer and printer may or may not breakdown. Each equipment is described by its current state (state: {OK, NOK}). For computers, an additional attribute shows if it can print (canPrint:{can, cannot}). Power supplies are described by their power state (power: {true, false}). Finally, a computer is usually plugged to one or more printers; it can print if at least one of its printers is functional. The printer can be functional, malfunctioning or broken.
2. Steps for creating the Power Surge
In this example, we will be using the prm_run interpreter. You could also use pyAgrum or directly aGrUM. For simplicity we will declare all types, interfaces, classes and systems in a single file. However, for large projects you should split elements in different files.
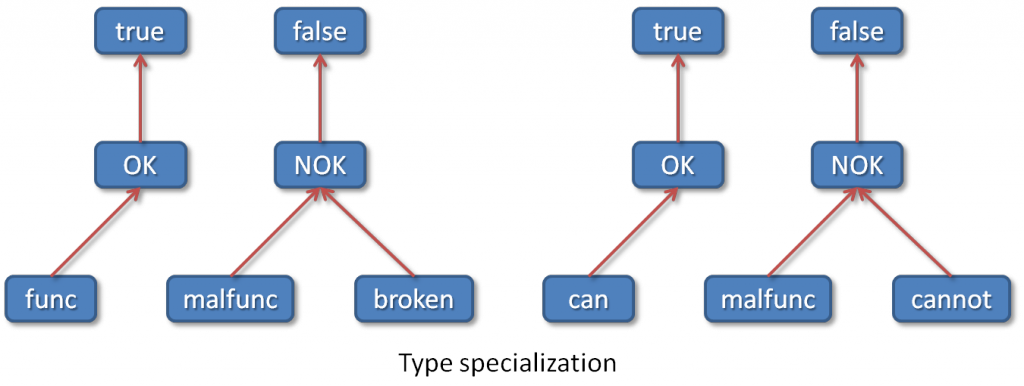
We will first declare the different types used in our example, not that the boolean type is (the only) predefined type in the O3PRM language.
// Generic Type (for all devices)
type t_state OK, NOK;
// Type specific to printers extended from the generic type
type t_steteDegraded extends typeState
broken : NOK,
malfunc : NOK,
func : OK;
// Type specific to computers extended from the generic type
type t_canPrint extends typeState
cannot : NOK,
malfunc : NOK,
can : OK;
New, we declare each class of our example.
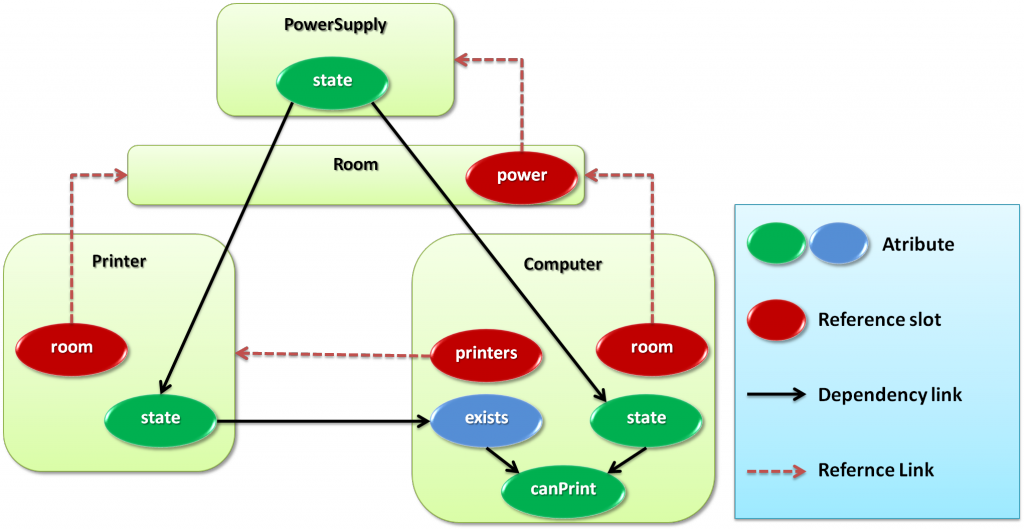
PowerSupply class:
// This is a basic class with a simple CPT
class PowerSupply {
// CPT is similar to {[NOK,OK]}
t_state state {[0.01,0.99]};
}
Ink class:
class Ink {
// Boolean variables [false, true]
boolean state {[0.01 ,0.99]};
}
Room class:
class Room {
// Reference slot
PowerSupply powerSupply;
}
Device class:
class Device {
// Reference slot
Room room;
t_state state dependson room.powerSupply.state {
// false | true
[ 0.99, 0.01, // false
0.01, 0.99] // true
};
}
Printer class :
class Printer extends Device {
boolean hasPaper {[0 , 1]};
//Array of reference slots
Ink[] ink;
//The function forall is detailled in O3prm syntax
boolean hasInk = forall ([ink.state], true);
// the state of the printers depends on : the room power supply,
// the ink and the presence of the paper
typestateDegraded state dependson room.powerSupply.state, hasInk, hasPaper {
// false | true |
// false | true | false | true |
// false | true | false | true | false | true | false | true |
[ 0.98, 0.98, 0.98, 0.98, 0.98, 0.90, 0.95, 0.01, // broken
0.01, 0.01, 0.01, 0.01, 0.01, 0.09, 0.04, 0.01, // malfunc
0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.01, 0.98 ] // func
};
}
Computer class:
class Computer extends Device {
Printer[ ] printers;
boolean hasPrinters = exists ([printers.state], func);
typeCanPrint canPrint dependson room.powerSupply.state , hasPrinters {
// false | true
// false | true | false | true
[ 0.98, 0.98, 0.90, 0.01, // cannot
0.01, 0.01, 0.09, 0.01, // malfunc
0.01, 0.01, 0.01, 0.98 ] // func
};
}
When the relational skeleton contains all its items, we can instantiate all the objects of the real system.
system Print {
PowerSupply power;
// all ink colours: black, yellow, magenta and cyan
Ink B;
Ink Y;
Ink M;
Ink C;
// 4 rooms
Room[4] rooms;
// adding the appropriate powerSupply to the printer room1
rooms.powerSupply = power;
// Printer "colour" 1
Printer pc1;
pc1.room = rooms[0]; // adding the appropriate room to the printer pc1
pc1.ink += B; // adding ink "blue" to the printer pc1
pc1.ink += Y;
pc1.ink += M;
pc1.ink += C;
// Printer "Black and white"
Printer pBW1;
pBW1.room = rooms[3];
pBW1.ink += B;
// Printer "colour" 2
Printer pc2;
pc2.room = rooms[3];
pc2.ink += B;
pc2.ink += Y;
pc2.ink += M;
pc2.ink += C;
// Printer "colour"3
Printer pc3;
pc3.room = rooms[3];
pc3.ink += B;
pc3.ink += Y;
pc3.ink += M;
pc3.ink += C;
// Computer 1
Computer c1;
c1.room = rooms[0]; // adding the appropriate room to the computer c1
c1.printers += pc1; // adding the printer pc1 to the computer c1
// Computer 2
Computer c2;
c2.room = rooms[1];
c2.printers += pBW1; // adding the connected printers to the computer c2
c2.printers += pc2;
c2.printers += pc3;
// Computer 3
Computer c3;
c3.room = rooms[1];
c3.printers += pBW1;
c3.printers += pc2;
c3.printers += pc3;
// Computer 4
Computer c4;
c4.room = rooms[2];
c4.printers += pBW1;
c4.printers += pc2;
c4.printers += pc3;
}
The last step is to create the request file in order to execute the modelled system and obtain the availability of the requested equipment/equipments.
Example 01:
import printers;
request PrintRequest {
// engine of computing inference
engine SVE;
// computer 1 can print
printers.Print.c1.canPrint = can;
// let's check if computer 2 can print
? printers.Print.c2.canPrint;
}
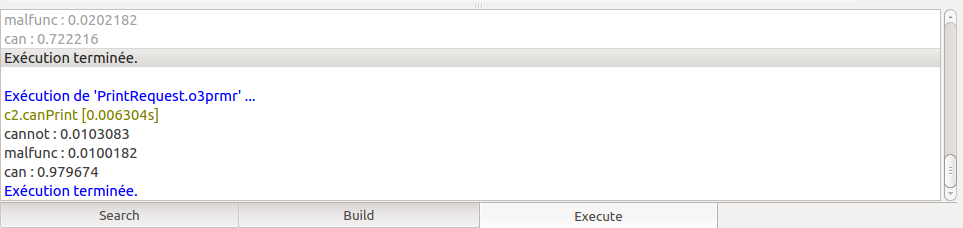
Executing prm_run over this exemple yield the folowing results:
Example 02:
import printers;
request PrintRequest {
// engine of computing inference
engine SVE;
// computer 1 cannot print
printers.Print.c1.canPrint = cannot;
// let's check if computer 2 can print
? printers.Print.c2.canPrint;
}
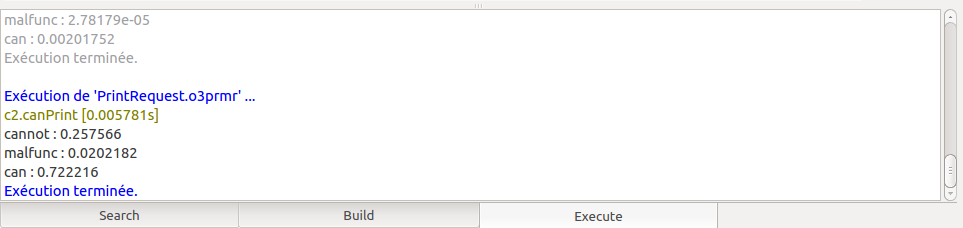
In the second example, we see that the possibility of printing by the second computer is forced down from 97% to 72% knowing that the first computer cannot print.
To download the example of printers click here.
